Regular \$2, for you \$3: when a discounted transfer is not a discount
Oftentimes there are discounts for transferring between transit routes. For instance, in Boston, when you pay \$1.70 to ride a bus, you get a \$1.70 discount off the subway fare and only pay \$0.70 instead of \$2.40 when transferring. In Suffolk County, New York, once you pay \$2.25 for a bus, you save \$2.00 off the next bus fare (you have to pay \$0.25 for a transfer slip). Most transit systems rely on transfers, and this is a good thing, but to make such a network work without thumbing your nose at riders, you have to provide free transfers.

Transferring between buses usually provides a discount, but could cost more in some cases.
So far, so good. We discount subsequent rides after riding the first vehicle to make the system more efficient and to not penalize riders who don’t happen to be traveling somewhere where they can get in a single ride. Sounds like a good plan.
But the road to hell is paved with good intentions. In some cases, these discounted transfers are actually negative: that is, after riding some set of transit vehicles, it is actually more expensive to ride the next set than it would be if there were no discounted transfers. Here are three examples:
In Boston, a local bus costs \$1.70, an express bus costs \$4.25, and the subway costs \$2.40. Transferring from a local bus to an express bus gives a \$1.70 discount on the express bus, and transferring from an express bus to the subway is free. You can only use one discounted transfer; on the third ride you need to pay again. So the full fare for this journey will be \$1.70 for the local bus, \$2.55 for the express bus, and \$2.40 for the subway—a total of \$6.65. But if you were to lose your transfer slip1 after riding the local bus, you would pay \$1.70 for the local bus, the full fare of \$4.25 for the express, and get a free transfer to the subway—a total of only \$5.95! So the transfer discount afforded by the first ride in this journey is actually -\$0.70.
In New York, a local bus costs \$2.75, and an express bus costs \$6.75. If you transfer from a local bus to another local bus it is free; if you transfer to an express bus, you save \$3.00 on the express bus fare (yes, it’s cheaper to ride a local bus then an express bus than it is to just ride the express bus alone). As in Boston, you only get one discounted transfer. So a trip that requires a local bus followed by a local bus followed by an express bus, you would pay \$2.75, get a free transfer to the second bus, and then pay \$6.75 full fare for the express bus—a total of \$9.50. But if you were to lose your ticket2 after riding the first local bus, you would pay \$2.75 for the first local bus, then \$2.75 for the second one since you lost your transfer, and then pay only \$3.75 for the express bus—a total of only \$9.25! The transfer discount afforded by the first ride in this journey is -\$0.25.
Similarly in New York, there is a free transfer from an express bus to another express bus, if you paid full fare when boarding the first express bus. So a local bus to express bus to express bus trip costs \$2.75 plus a \$3.75 upgrade to the second express bus plus \$6.75 full fare for the last express bus—a total of \$13.25. However, if one were to lose one’s transfer allowance after riding the local bus, the cost would be \$2.75 for the local bus plus \$6.75 full fare for the first express bus, with a free transfer to the second express bus—a total of only \$9.50! The first ride provides a transfer discount of -\$3.75.
Many commuter rail systems operate a local-express service pattern during peak hours. Trains will run local service for outlying parts of the line, and then express to the downtown terminals at some point. People traveling from outlying stations to local stations near downtown will need to transfer from the local-express service to a local service at an intermediate point. While these are rarely documented as discounted transfers, it’s generally assumed that if you buy a ticket between such stations, you can make the transfer without paying a new fare. If there is ever a situation where the sum of the two fares between an origin station, an intermediate station, and a destination is less than the fare from the origin to the destination, at the intermediate station the transfer discount is negative—the rider would be better off buying a ticket to an intermediate point, and then buying another ticket to their destination.
This is in fact already the case for one specific location in the Boston commuter rail system: Quincy Center. In 2018, Quincy Center was assigned to a special Zone 1A/1 fare zone, where trips into Zone 1A (central Boston) cost \$2.25, while trips to any outlying area cost the same as if Quincy Center had been in Zone 1 (the first zone outside of Central Boston). A full-fare journey from South Station in Central Boston to Braintree in Zone 2 was \$6.75, while a ticket from South Station to Quincy Center is \$2.25 and another ticket from Quincy Center to Braintree was \$3.25, a total of \$5.50. At Quincy Center, the transfer “discount” from continuing with the same ticket on the commuter rail system is -\$1.25.
Riders might be able to realize such a journey without getting off the train at the intermediate point, especially if they were to move to a different car, put on a hat or mustache, etc.3 While it might not be encouraged, few transit systems would be able to enforce a rule that prevented customers from getting off the train and boarding the next one with a new ticket.4 Customers could always say they stopped to run an errand.
This scenario of two tickets being cheaper than a single ticket covering the whole journey is not common, but can arise when testing regional rail scenarios, as Anson Stewart and I did in a recent paper. We created a low-fare zone for all trips on commuter rail in Boston and its inner suburbs, while maintaining existing fares outside this zone. Consider a trip from Back Bay (Zone 1A) to Framingham (Zone 5). The full fare for this trip at the time we wrote the paper was \$9.25. With the regional rail scenario, one could spend \$2.75 to get from Back Bay to Auburndale, and then \$4.00 from Auburndale to Framingham, a total of \$6.75. We did not allow discounted transfers between commuter rail trains, so this was not an issue, but if we had, it would have been.
So what, you might say. Certain trips cost a bit more than they would if you did something tricky with losing your transfer slip. Maybe a few folks have figured this out and have two electronic fare cards that they use for different parts of the trip, and others just pay a bit more than they truly have to for trips. This isn’t necessarily unjust—it depends on who is making these trips.
But it is a problem for the algorithm Anson Stewart and I developed for finding the lowest-cost trips. One of the assumptions in that paper is in equations 4 and 5, where we assume that transfer discounts are nonnegative. At the time we wrote the paper, we assumed that to generally be true, and just noted that some trips with these edge cases could be missed by the algorithm. But now it seems that such negatively-discounted transfers are actually fairly common.
I see three possible courses of action. One is to just not worry about this problem, and assume that trips where it comes into play are strange, and it’s okay if the algorithm doesn’t always find the cheapest trip in these cases. Another is to implement code that figures out when it is advantageous to discard a transfer allowance, and does so. The final way is to remove the nonnegativity assumption for transfer discounts in the algorithm.
I don’t think teaching the algorithm to discard transfer allowances when it is advantageous to do so is a good option. Most system users just scan their smartcard when they board and don’t do a lot of math to figure out if a complex, ad-hoc combination of multiple fares would yield a cheaper price. Furthermore, agencies probably don’t want to base equity analyses on fare rules that require riders to do something tricky with multiple smartcards. I’m a PhD candidate in transport geography, and I’ve spent a lot of time thinking about fares, and I’ve only just figured these out. Agencies can’t base their analysis on requiring that people go through months of mathematical gymnastics to save a few bucks.
Just not worrying about it is probably appropriate in most systems, where these trips are quite rare. However, if they are common, removing the nonnegativity assumption may be warranted. This is not that difficult, although it will reduce performance as more paths will be retained.
Theorem 3.1 in the paper states that one route is better than another if its cumulative fare is less than the cumulative fare minus maximum discount of another route. This can be recast as one route is better than another if its cumulative fare minus minimum (i.e. most negative) discount is less than the cumulative fare minus maximum discount of the other route (keeping in mind that subtracting a negative number makes the result larger). Conceptually, this means that we consider a route better than another if the amount you’ve paid plus the largest increment on top of full fare that you might have to pay is less than the amount paid for the other route minus the most you could save from taking the other route.
This also requires making sure that having a transfer allowance for the purposes of Theorem 3.2 is not considered superior to not having a transfer allowance if there is any chance the transfer allowance provides a negative discount. Where this creates a significant performance hit is when dealing with transfer allowance expiration: while the algorithm currently assumes that a transfer allowance with more time remaining is preferable, if that transfer allowance is negative for some journeys, the transfer allowance with less time remaining may be better. If the transfer expiration period is more than the maximum travel time you are using in your accessibility metric, though, the optimization described in Section 3.4 of the original paper will apply and ameliorate this problem.
Making this change will mean that when there are negatively-discounted transfers, the algorithm will do everything in its power to get rid of them, for instance by riding random buses one stop just to use up the remaining value. Consider this example:
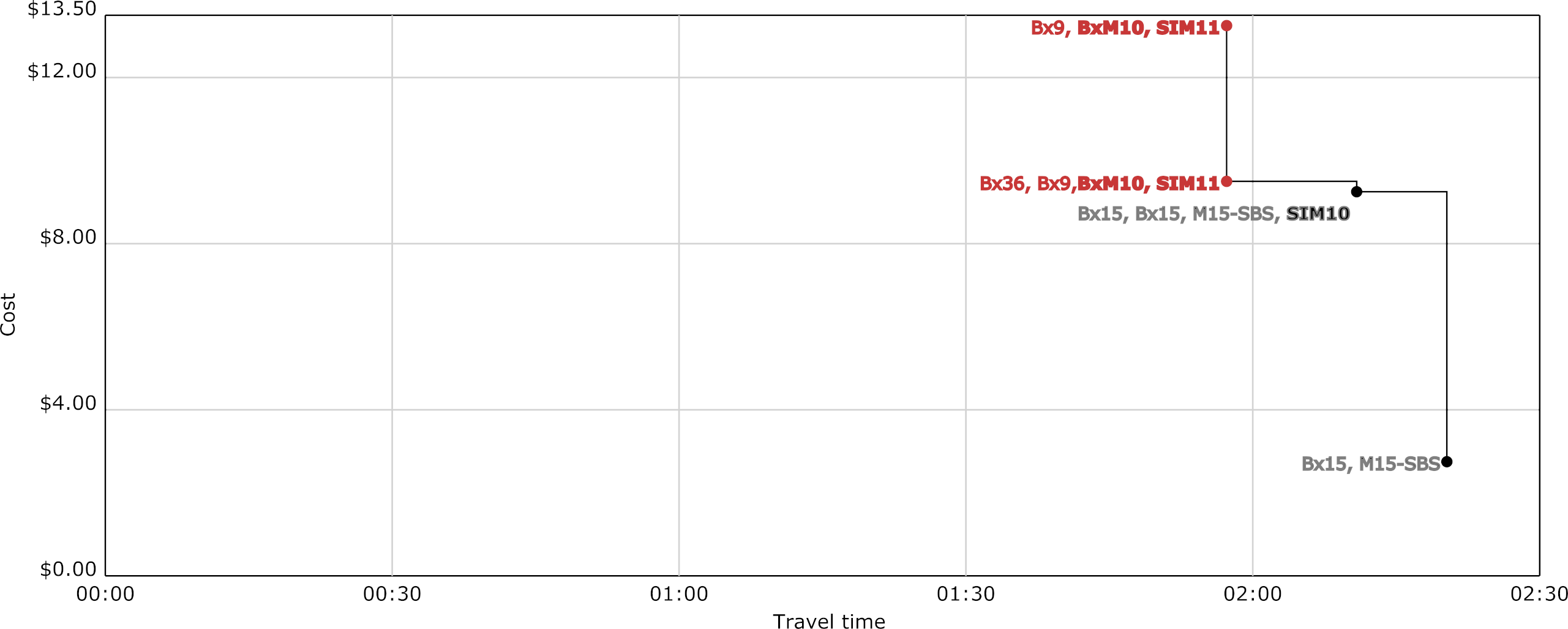
Tradeoff surface for travel by bus from 3rd Ave and E 180th St in the Bronx to Lower Manhattan
This is a Pareto surface. Along the x axis is travel time, and along the y axis is travel cost. The points on the plot are all the Pareto-optimal options for bus travel between 3rd Ave and E 180th St in the Bronx and Lower Manhattan. That is, there are no options that are both faster and cheaper than any of the options on this surface. Express buses are shown in bold.
Let’s consider the two options tied for fastest, which are shown in red. They both take the Bx9 local bus and transfer to the BxM10 express bus at Morris Park Ave/E 180th St and then to the SIM111 to get to lower Manhattan. However, the cheaper option adds a short ride on the Bx36, so that two local buses have been ridden and the transfer allowance has been cleared before boarding the express bus. The two options are on a map below, with the added ride on the Bx36 shown in red.
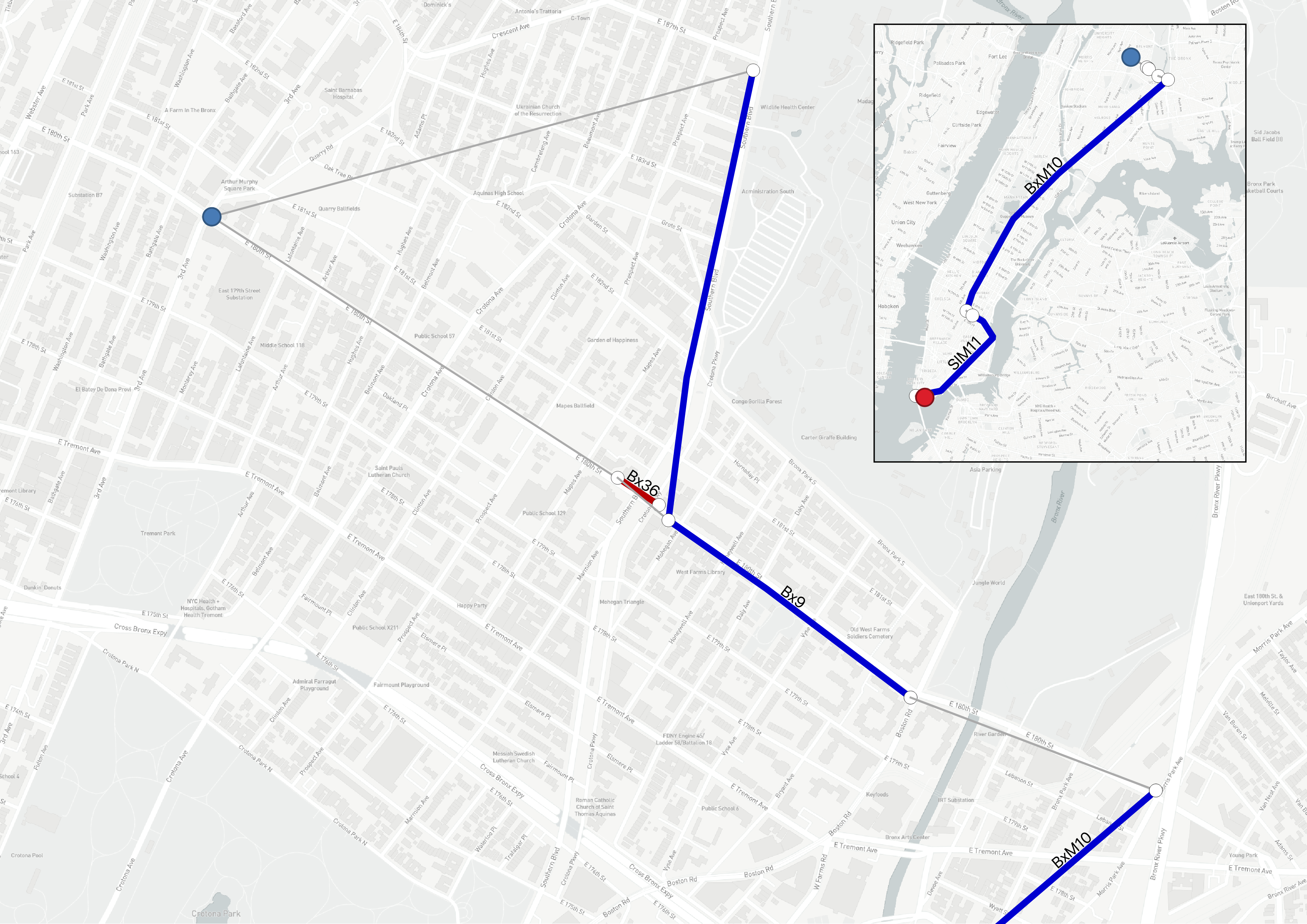
Map showing differences between two fastest options. Map data © OpenStreetMap contributors, map tiles © Mapbox
The algorithm as it exists does not find the cheaper path in this case, because at the boarding stop for the express bus, the cumulative fare paid for the cheaper 2-bus option is \$2.75 and the maximum transfer allowance is zero. Since the cumulative fare paid for the more expensive option is also \$2.75, Theorem 3.1 concludes that the 2-bus option cannot yield a cheaper trip, and prunes it. To produce the Pareto surface, I had to modify the algorithm to disable Theorem 3.1, and not consider having a transfer allowance to be better than not having one in Theorem 3.2.
Since the router is finding trips that are Pareto-optimal in terms of time and fare, it will retain both trips if the more expensive one is faster. In this case, the router can sneak in an extra bus ride without missing the express bus, so the cheaper option has the same travel time.
I’m not sure it’s worth the trouble to support these negative transfer allowances properly. In the same vein as not basing our analysis on people doing tricky things where they intentionally discard their transfer slips, I’m not sure we should base our analysis on assuming people will do things like ride a bus one stop to consume their transfer allowance. Even without modifications to the router, it will sometimes find these cheaper trips that come from using negative transfer allowances—for instance, if the two options do not board the express bus at the same stop, they will not be compared—so not handling these edge cases can create some inconsistencies in terms of whether the absolute cheapest trip is always found. But I would argue these inconsistencies are minor enough that they can be ignored in most cases.
The MBTA actually uses an electronic fare card, so losing your transfer slip is not really possible, but suppose you had two CharlieCards and used the second one for the second boarding ↩︎
Similar to Boston, New York uses an electronic fare card. ↩︎
The author has actually done this on Amtrak, although not to save money, and he did not attempt to cover up that he had bought two separate tickets for the same train. ↩︎
The author has done this as well—when I lived in DC I had a WMATA SelectPass which meant that every subway ride under \$2.35 was free, and after \$2.35 I would pay the difference. Sometimes if I was not in a hurry I would get off the train, tag out and back into the station, and board the next train, turning a \$2.75 trip into two free \$2.35 trips. ↩︎